Lernen von KI-Anwendungen
Generative KI schleicht sich zunehmend in fast jede Aufgabe ein, an der ich heutzutage arbeite, also ist es an der Zeit, …

Schon vor einer Weile ist mir das Buch -The Math(s) Fix- von Conrad Wolfram über den Weg gelaufen. Ich konnte damals nur kurz hineinschauen, aber die Grundideen zum Thema rechnerisches Lernen hatten mich gleich angesprochen.
Nun konnte ich mich endlich intensiver mit dem Konzept auseinandersetzen und bin durchgehend begeistert von der Art, wir Wolfram das Thema angeht, die Probleme der heutigen Mathematiklehre auf’s Korn nimmt und gezielt der curricularen Blockade, die wir seit Jahrzehnten haben, ein neues Konzept entgegenstellt, dass zeigt, worauf es wirklich ankommt.
Die Herleitung basiert auf der Erkenntnis, dass der Nutzen von Mathematik bzw. von rechnerischem Denken nicht im Auswendiglernen von Themengebieten und Formeln liegt, sondern in der gekonnten Anwendung im Problemlösungsprozess. Wolfram weist darauf hin, dass der Prozess wie oben im Bild dargestellt immer 4 Phasen durchläuft:
Bevor ich also -auch als Lernender- eine Matheaufgabe löse, muss ich erst einmal ein Problem haben, dass mich wirklich beschäftigt. In der Definitionsphase kann dann Domainwissen gesammelt und geordnet werden, sowie erste Fragen entstehen, was denn genau das zu lösende Problem ist.
In der Abstraktionsphase wird dann versucht, die Fragestellung so zu abstrahieren, dass eine berechenbare Form entsteht. Dazu gehört neben den klassischen Formeln und Konzepten der Mathematik auch Computeralgorithmen oder statistische Verfahren aus den Datenwissenschaften. Wer sich mit Konzepten und Werkzeugen auskennt, findet hier schnell ein Vorgehen. Da, wie wir gleich sehen werden, nicht jeder Algorithmus oder jede Formel tief verstanden sein muss, reicht allerdings auch die Fähigkeit, durch Suchen in Wissensbasen oder im Web eine Vorgehensweise zu wählen, die im nächsten Schritt angewendet werden kann.
Nachdem der Algorithmus klar ist, kann gerechnet werden. Wolfram weist darauf hin, dass ironischerweise heute in den Schulen nur dieser Schritt wirklich ernsthaft eingeübt wird - leider zu Unrecht, da schematisches Rechnen per Hand natürlich im Zeitalter der Computerisierung eigentlich gar keine Rolle mehr spielt. Idealerweise wählen wir eine computerbasierte Lernplattform mit mathematischer Unterstützung, um unser formal definiertes Problem nun in Code umgesetzt ablaufen zu lassen.
Zum Abschluss müssen die Ergebnisse interpretiert werden. Sind die berechneten Ergebnisse plausibel? Gibt es Konfidenzintervalle, in denen das Ergebnis bzw. die Prozedur die besten Ergebnisse liefert? Lässt sich der Algorithmus verbessern oder erweitern? Welche Erkenntnisse kann ich für die nächste Iteration in der Problemlösung gewinnen? Die Ergebnisse haben also unmittelbar Praxisbezug, was für eine ungeahnte Motivation bei den Lernenden sorgt. Der gesamte mathematische Lernpfad ist eine Spirale des immer weiter schreitenden Konzepts dieser 4 Schritte, hier heißt das “Superprozess”. Jedes Ergebnis sorgt als Input für die nächste Stufe für eine immer breiter werdende Problemlösungskompetenz.
Wolfram gliedert sein Konzept im Folgenden fein auf und so entsteht ein komplettes didaktisches anwendbares Modell, das nebenbei auch das klassische Curriculum hinwegfegt. Die Grundidee ist, Lernenden die Themen nicht nach Schwierigkeit des Rechenprozesses nahebringen zu wollen, sondern nach Schwierigkeit des zugrundeliegenden Problems. Das ist so naheliegend, dass man sich fragen muss, warum in den klassischen Bildungseinrichungen noch niemand darauf gekommen ist. Natürlich gibt es auch hier eine Gliederung der Themen - allerdings nicht zum Selbstzweck, sondern um die Orientierung im Abstraktionsprozess zu erleichtern. In 3 Fertigkeitsstufen kommen als Vorschlag 5 Themengebiete zur Sprache, die natürlich immer wieder revisioniert werden können:
Also nicht die “reine Lehre” akademischer Curricula, sondern enge Verflechtung mit Anwendbarkeit und digitalen Technologien.
Wolfram kommt zu der Erkenntnis, dass eine konstruktivistische Pädagogik Vorrang haben sollte vor einer instruktionellen, jedoch fordert er, Basiskonzepte durchaus begleitet zu lehren, damit der Gesamtprozess gut in Gang kommt. Wer nicht weiß, was er nicht weiß, tut sich schwer, gute Lösungen zu erhalten, so ist dieser Ansatz sicher eine gute Verbindung von selbstbestimmter Problemlösung und didaktisch vermitteltem Basiswissen.
Lehrer werden bei ihm “CEO of the classroom” genannt, also nicht primär Alleswissende, sondern eher verantwortlich für das Gelingen des Gesamtprozesses. Das umfasst, die Grenzen des eigenen Wissens zu erkennen und Experten hinzuzuziehen wenn nötig, und auch die analytischen Fähigkeiten der Lehrenden in Bezug auf die Prozesse der Lernenden sind eine wichtige Kompetenz, die heute viel zu kurz kommt. Nicht überraschend kommt Wolfram zu der Erkenntnis, dass es eine neue Lehrerausbildung braucht.
Im dritten abschließenden Teil des Buchs kommt dann Transformationsbetrachtung an die Reihe. Wie kann der Wandel zu so einer neuen Art der mathematischen Ausbildung erfolgen? Er steigt konsequent in der politischen Steuerung ein, die heute eine Modernisierung verhindert. Damit das gelingt, braucht es eine Bewegung, die er in diesem Zusammenhang versucht, global auf die Beine zu stellen - The Maths Fix Campaign for Core Computational Curriculum Change (MFC5). Ganz praktisch rundet seine Website computerbasedmath.org das Konzept mit einer konkreten Lern- und Lehrplattform ab, wo auch viele der Inhalte des Buchs dargestellt und mit Beispielen anschaulich gemacht werden.
Fazit: rundum gelunge Neuausrichtung von Mathematikausbildung. Mich hat die Lektüre des Buches zusätzlich zu meiner Konzeptarbeit am Schuldesignbaukasten dazu animiert, einen Bildkalender für 2024 (mit KI-generierten Bildern 😎) zu gestalten, der in Kürze im Handel oder jetzt schon bei mir in verschiedenen Größen erhältlich ist.



Generative KI schleicht sich zunehmend in fast jede Aufgabe ein, an der ich heutzutage arbeite, also ist es an der Zeit, …
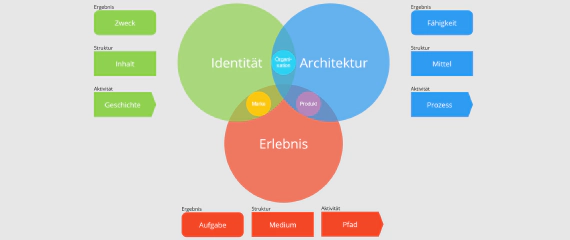
Neue Schulen braucht das Land! Nachdem die von mir mitgegründete Freie Schule Ostfriesland inzwischen seit einigen …
Ob in der freien Schule oder als Selbstlernende:r,
entwickle deine persönlichen Fähigkeiten weiter, online und global. Ab 8 Jahren.