A while ago I came across the book -The Math(s) Fix- by Conrad Wolfram. I was only able to take a quick look at it at the time, but the basic ideas about computational learning appealed to me right away.

Now I finally had the chance to take a closer look at the concept and I am very enthusiastic about the way Wolfram approaches the topic, takes aim at the problems of today’s mathematics teaching and specifically opposes the curricular blockade we have had for decades with a new concept that shows what really matters.

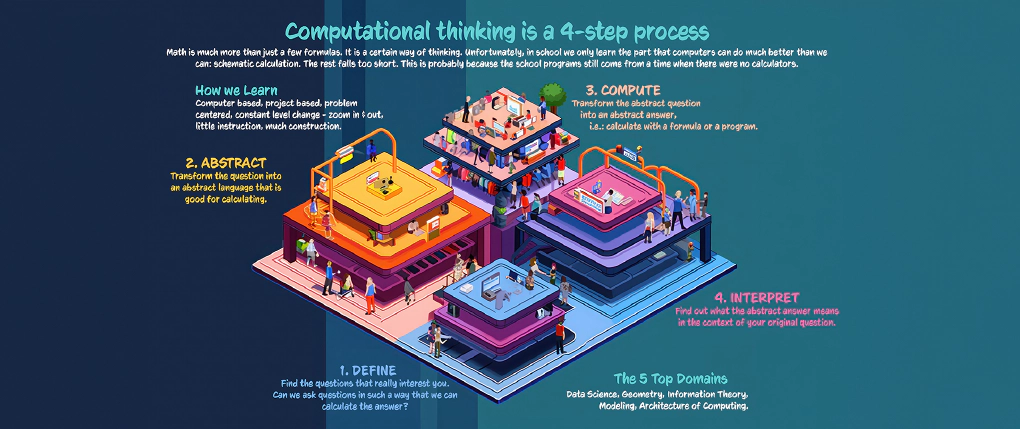
The derivation is based on the realization that the benefit of mathematics or of computational thinking does not lie in the memorization of topics and formulas, but in the skillful application in the problem-solving process. Wolfram points out that the process always goes through 4 phases as shown in the picture above:

1. Definition
2. Abstraction
3. Calculation
4. Interpretation

So before I -also as a learner- solve a math problem, I first have to have a problem that really concerns me. In the definition phase, domain knowledge can be collected and sorted, and first questions can be asked, what exactly is the problem to be solved.

In the abstraction phase, an attempt is then made to abstract the problem in such a way that a calculable form is created. In addition to the classical formulas and concepts of mathematics, this also includes computer algorithms or statistical methods from the data sciences. Those who are familiar with concepts and tools will quickly find a way to proceed. Since, as we will see in a moment, not every algorithm or formula needs to be deeply understood, however, the ability to select a procedure by searching knowledge bases or the web is also sufficient to apply in the next step.

After the algorithm is clear, calculations can be done. Wolfram points out that, ironically, only this step is really practiced seriously in schools today - unfortunately unjustly, since schematic calculation by hand is, of course, no longer really relevant in the age of computerization. Ideally, we choose a computer-based learning platform with mathematical support to run our formally defined problem now implemented in code.

Finally, the results have to be interpreted. Are the calculated results plausible? Are there confidence intervals in which the result or procedure gives the best results? Can the algorithm be improved or extended? What insights can I gain for the next iteration in the problem solution? Thus, the results have immediate practical relevance, which provides unprecedented motivation for learners. The entire mathematical learning path is a spiral of the ever-advancing concept of these 4 steps, here called “super process”. Each outcome, as input to the next step, provides ever broadening problem solving skills.

Wolfram breaks down his concept finely in the following and thus a complete didactic applicable model emerges, which incidentally also sweeps away the classical curriculum. The basic idea is to teach learners not according to the difficulty of the computational process, but according to the difficulty of the underlying problem. This is so obvious that one has to wonder why no one has thought of it in the classical educational institutions. Of course, there is also a structuring of the topics - however, not as an end in itself, but to facilitate orientation in the process of abstraction. In 3 skill levels, 5 topics come up as a suggestion, which of course can always be revised:

• Data Science
• Geometry
• Information Theory
• Modeling
• Architecture of Computation

Thus, not the “pure teaching” of academic curricula, but tightly intertwined with applicability and digital technologies.

Wolfram comes to the conclusion that a constructivist pedagogy should take precedence over an instructional one, but he demands that basic concepts be taught in an accompanied manner so that the overall process gets off to a good start. If you don’t know what you don’t know, it’s hard to get good solutions, so this approach is certainly a good combination of self-determined problem solving and didactically taught basic knowledge.

Teachers are called “CEO of the classroom” in his approach, i.e. not primarily know-it-all, but rather responsible for the success of the overall process. This includes recognizing the limits of one’s own knowledge and calling in experts when necessary, and the analytical skills of teachers in relation to the processes of the learners are also an important competence that is much neglected today. Not surprisingly, Wolfram concludes that a new teacher education is needed.

In the third concluding part of the book, transformational considerations take their turn. How can the transformation to such a new kind of mathematical education take place? He consistently gets into the political control that today prevents modernization. For this to succeed, it will take a movement that he is trying to get off the ground globally in this context - The Maths Fix Campaign for Core Computational Curriculum Change (MFC5). In practical terms, his website computerbasedmath.org rounds out the concept with a concrete learning and teaching platform, where much of the book’s content is also presented and illustrated with examples.

Conclusion: an all-around successful reorientation of mathematics education. Reading the book has encouraged me to design a picture calendar for 2024 (with AI-generated pictures 😎), which will soon be available in stores or is already available from me now in various sizes (images show german version but translation is possible).